Zurück zur Inhaltsangabe
2. Kryptographische Lösungen
Das Hauptaugenmerk richtet sich hierbei auf das Kodieren und
Dekodieren von Daten. Nur dem Empfänger sollte es möglich
sein, die Daten zu entziffern und nicht von dritten Personen. Ferner
sollten die kodierten Daten vom Sender signiert sein, so dass
der Empfänger sicher sein kann, dass die Daten wirklich von
diesem Sender kommen,
der Sender die geschickten Daten später nicht mehr abstreiten
kann und
der Empfänger nicht die vom Sender erhaltende Signatur benutzen
kann, um Daten zu signieren.
Systeme die solche kryptographischen Lösungen realisieren
benutzen meist Schlüssel. Diese werden benutzt um eine Nachricht M
in eine chiffrierte Nachricht H zu kodieren. Später wird diese
Nachricht H zu der ursprünglichen Nachricht M dekodiert.
2.1 Symmetrische Kryptosysteme
Diesem Symmetrischen Verschlüsselungsverfahren wird auch als
Private-Key-Verfahren bezeichnet. Der Absender A kodiert die Nachricht
mit einem geheimen Schlüssel Kpriv. Somit wird die Nachricht für
niemanden außer dem Empfänger verständlich, der den
gleichen Schlüssel Kpriv besitzen muss.
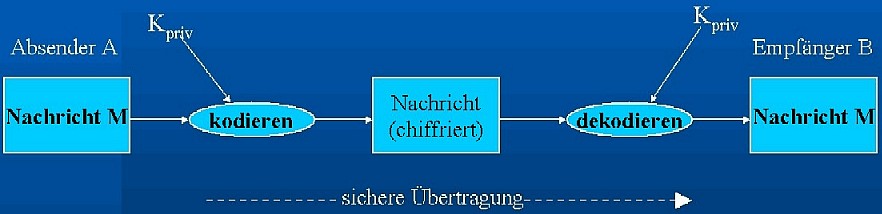
Ein Beispiel dafür ist DES (Data
Encryption Standard)
Bei DES handelt es sich um ein symmetrisches Verfahren, wobei der
Algorithmus mit der sogenannten Produktverschlüsselung arbeitet,
bei der als elementare Verschlüsselung Subsitutionen und
Transpositionen (Permutationen) verwendet werden.
Der DES-Algorithmus wurde erstmals 1974 von der US Regierung veröffentlicht
und ist als ANSI-Standard normiert (ANSI X3.92-1981). Es handelt sich um
einen Blockalgorithmus, welcher 64 Bits Klartext in 64 Bits Schlüsseltext
und umgekehrt überführt. Die Schlüssellänge beträgt
ebenfalls 64 Bit, wobei jedoch nur 56 Bit hiervon signifikant sind. DES
lässt sich sowohl hardwaremäßig, wie auch softwaremäßig
implementieren. Bei den neuesten Hardware-Implemtierungen liegen die
Verschlüsselungsraten schon im Bereich GByte/s.
Eingesetzt wird das DES Verfahren insbesondere in Finanz-Applikationen
und kann als Quasi-Standard bezeichnet werden. DES ist zwar weit
verbreitet, allerdings nicht mehr zeitgemäß aufgrund der
geringen Schlüsselgröße von 56 Bit. Triple-DES (3DES)
erhöht die Sicherheit vom normalen DES-Verfahren, indem die Daten
mit doppelter (112 Bit) oder dreifacher (168 Bit) Schlüssellänge
verschlüsselt werden.
Zur Ablösung des DES wurde vor einiger Zeit der sogenannte
Advanced Encryption Standard (AES) ausgeschrieben, mit dem vor allem die
viel zu geringe Schlüsselgröße des DES der Vergangenheit
angehören wird.
Das Problem bei diesen Kryptosystemen besteht darin, dass es kaum
einen sicheren Weg gibt den Schlüssel zu übertragen. Schlüssel
müssen her persönlich ausgetauscht werden, was teuer und
zeitaufwendig ist. Außerdem werden Digitale Signaturen nicht berücksichtigt,
was dem Empfänger nie die Sicherheit gibt, dass die Nachricht vom
gewünschten Sender ist.
Um das Problem des Schlüsselaustausches zu lösen, wurde 1977
von Ron Rivest, Adi Shamir und Leonard Adleman,
das nach ihnen benannte RSA entwickelt. RSA ist ein sogenanntes
Public-Key-Kryptosystem.
Es werden hier statt einem Schlüssel, zwei Schlüssel
verwendet; ein öffentlicher Schlüssel (public) und ein
privater Schlüssel (private). Der private Schlüssel sollte
stets geheim gehalten werden, nur der öffentlich Schlüssel
wird jedem zugänglich gemacht.
Eine Nachricht die mit einem der beiden Schlüssel kodiert wurde
kann nur mit dem jeweiligen zweiten dekodiert werden. Die Grafik soll
dies verdeutlichen.
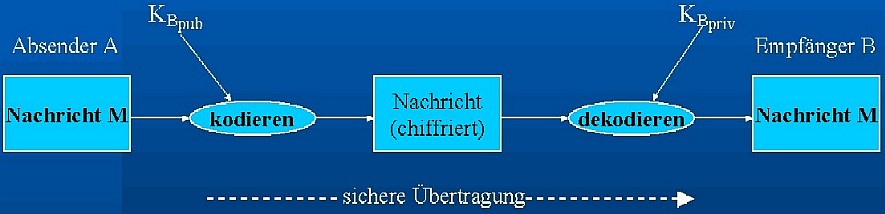
Die Sicherheit basiert auf der Schwierigkeit, eine große natürliche
Zahl zu faktorisieren. Bei entsprechend großem Schlüssel ist
eine Entschlüsselung (beim derzeitigen Stand der Technik und der
Kryptanalyse) nicht in einem akzeptablen Zeitraum möglich.
RSA hat zwei wichtige Vorteile gegenüber DES: Zum einen ist
sicheres Schlüsselmanagement möglich, ohne dass vorher private
Schlüssel ausgetauscht werden müssen. Ferner ermöglicht
RSA digitale Unterschriften, wie gleich erläutert wird.
Die Geschwindigkeit vom Public-Key-Verfahren hängt von der Größe
des Schlüssels ab. Damit arbeitet RSA um Größenordungen
langsamer als DES und eignet sich so nicht für
große Datenmengen. Bei einer DES-Implementierung in Hardware kann
sich der Geschwindigkeitsunterschied zwischen DES und RSA um einen
Faktor von 1.000 bis 10.000 unterscheiden. Zum Verschlüsseln großer
Nachrichten werden normalerweise RSA und DES kombiniert. Die Nachricht
wird mittels eines zufällig gewählten DES-Schlüssels
kodiert. Dieser Schlüssel wird mittels RSA kodiert und zusammen mit
der chiffrierten Nachricht verschickt.
2.3 Digitale Unterschriften
Digitale Unterschriften werden dadurch ermöglicht, dass man in
umgekehrter Reihenfolge der Schlüssel kodiert. D.h., es wird zuerst
mit dem privaten Schlüssel kodiert und später mit dem öffentlichen
Schlüssel dekodiert.
Wenn Absender A sein Dokument unterschreiben will, dann kodiert er
eine Signatur mit seinem privaten Schlüssel und verschickt dies an
den Empfänger B. Er dekodiert diese Signatur mit dem öffentlichen
Schlüssel von A. Es kann nur etwa sinnvolles herauskommen wenn die
Signatur von A stammt und nicht von Dritten verfälscht wurde.
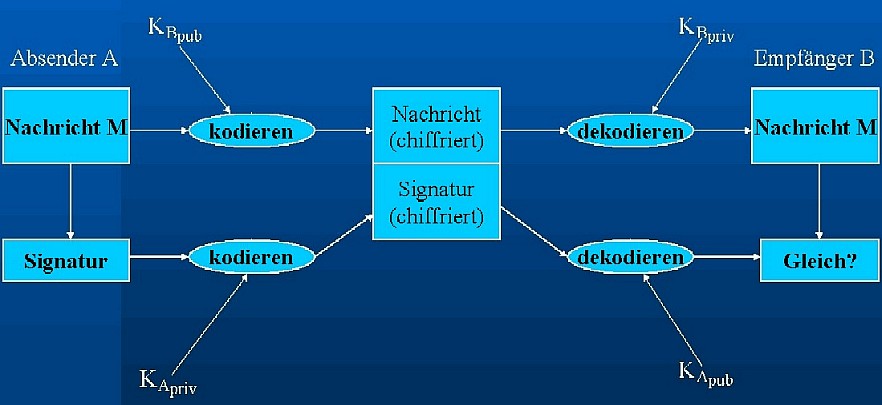
Eine Signatur wird normalerweise aus dem Dokument
mittels einer Einweg-Hash-Funktion, die man Message Digest
nennt, erzeugt. Es können keine Rückschlüsse auf das
Ausgangsdokument gemacht werden, außerdem ist es nicht möglich
aus zwei verschiedenen Dokumenten die gleiche Signatur zu erzeugen bzw.
es würde jeden realistischen Wert übersteigen.
Empfänger B hatte ja die Signatur von A erhalten und dekodiert.
um nun festzustellen, ob die Signatur und damit die Nachricht wirklich
von A stammen, berechnet B mittels der Einweg-Hash-Funktion nochmals des
Message-Digest und vergleicht diese mit der erhaltenen Message Digest.
Wenn sie beide gleich sind kann er sich sicher sein, dass die Nachricht
von A stammt, ansonsten wurde die Nachricht auf dem Transport verfälscht.
Beispiel: Message Digest 5 (MD5)
Message Digest 5 (MD5) ist eine von Ron Rivest erfundene
Einweg-Hash-Funktion. Sie generiert aus einer Nachricht, deren Länge
egal ist, eine 128-Bit lange Zahl. Es sind bisher keine zwei Texte
bekannt, die die gleiche MD5-Zahl erzeugen. Jede Änderung am Text lässt
eine erneute Überprüfung fehlschlagen.
2.4 Zertifikate für Schlüssel
Um die Gültigkeit von Schlüssel und deren Besitzer zu bestätigen,
brauchen Schlüssel in der digitalen Welt Zertifikate.
Zum Verwalten von diesen Zertifikaten und den öffentlichen Schlüsseln,
gibt es sogenannte Zertifikationsstellen (Key Certification Authority,
KCA).
Jeder Benutzer sollte ein Schlüsselpaar (öffentlichen und
privaten Schlüssel) selbst generieren. Den öffentlichen Schlüssel
übergibt er der KCA und erhält dafür ein Zertifikat.
Jeder, der diesen öffentlichen Schlüssel benutzen will, kann
diesen Schlüssel von der Zertifikationsstelle erhalten.
Beispiel: ISO X.509 Zertifikate
Das ISO X.509-Format ist ein Beispiel für eines von vielen
Formaten für Zertifikate von öffentlichen Schlüsseln.
Dieses Zertifikat enthält folgende Komponenten:
- Zertifikationsseriennummer
- Name der unterschreibenden Autorität
- Name des Besitzers des öffentlichen Schlüssels
- Gültigkeitszeitraum
- Der öffentliche Schlüssel selbst
- Unterschrift der Autorität
Zurück zur Inhaltsangabe


